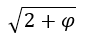If a spherical nucleus were at the center of a close-packed array of spheres in the icosahedron configuration, what would be its radius? That is, by how much must the nucleus shrink when the close-packed array jitterbugs from the VE to the icosahedron? Knowing that the icosahedron can be constructed from the three golden rectangles arranged orthogonally around a common center, it’s a simple matter of trigonometry.
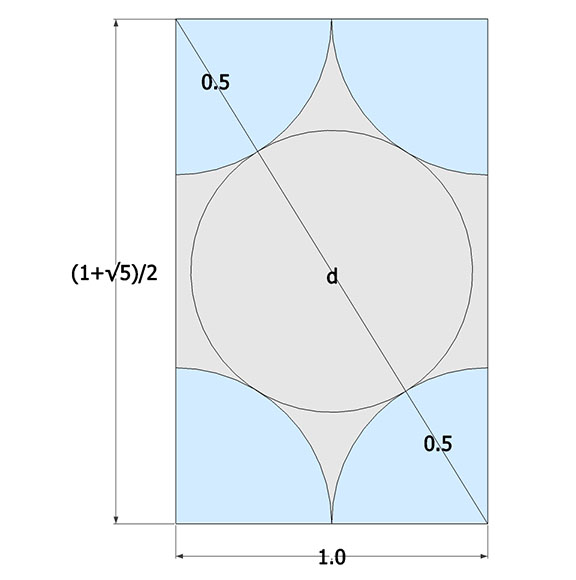
The diagonal (d) is the the square root of the sum of the squares of the two sides, or √(((1+√5)/2)+1²) ≈ 1.902113:
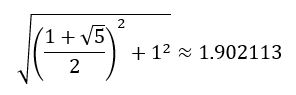
The diameter of the nucleus at the center of an icosahedron made up of unit-radius spheres is the length of the diagonal minus 1, or approximately 0.902113.
The golden ratio has some curious properties. For example, its square is equal to itself plus one:
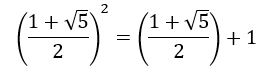
Knowing this, we can reduce the expression under the radical above to ((1+√5)/2)+2:
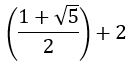
Since the expression on the left is the golden ratio, it follows that the diagonal of the icosahedron may be expressed as √(2+φ):
The Geometry of Thinking 