Spheres and Spaces

Greg Frederick

There is a revised version of this topic. See Spaces and Spheres (Redux).

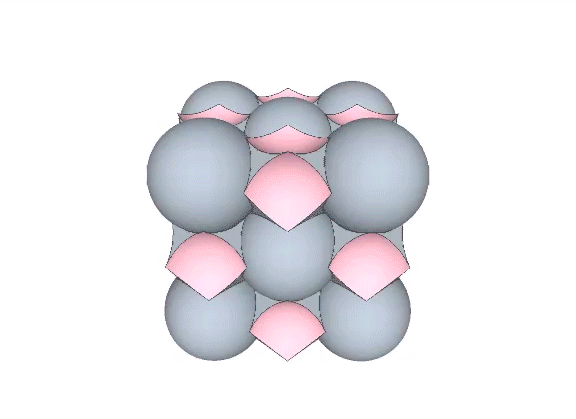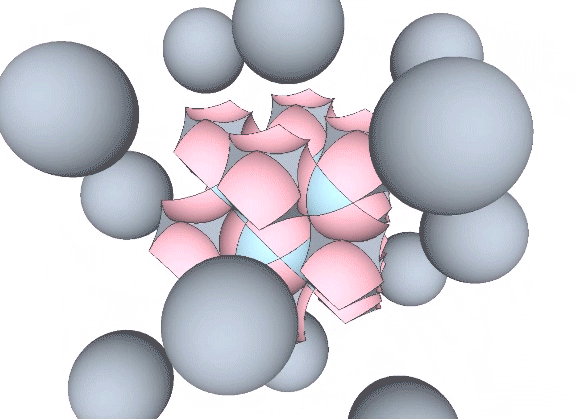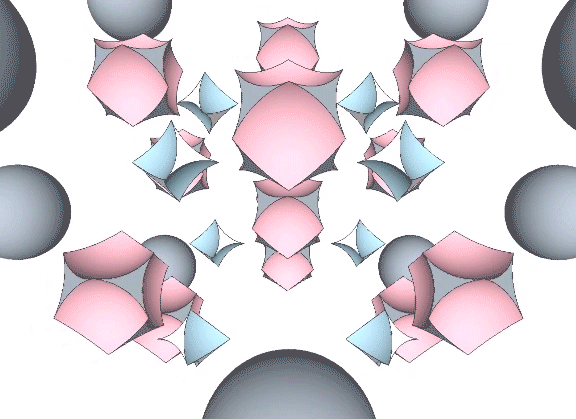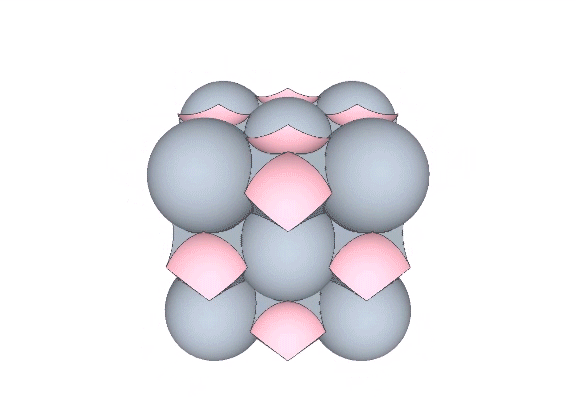
The isotropic vector matrix can be modeled as spheres, vectors, tensegrities, space-filling polyhedra, or as the concave polyhedra occupying the spaces and interstices between radially close-packed spheres. The space between radially close-packed spheres is a continuous web of concave octahedra and concave vector equilibria (VEs).

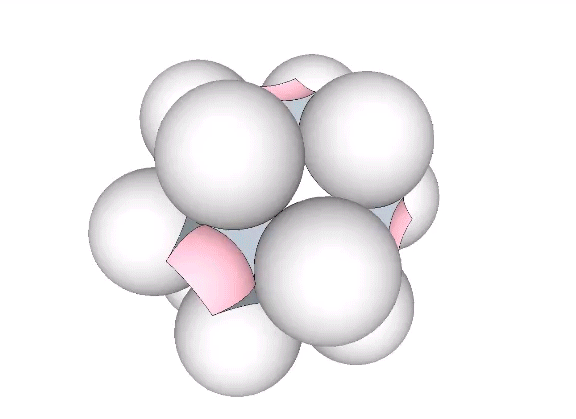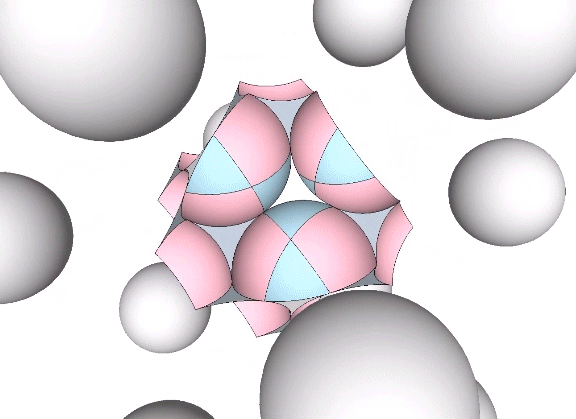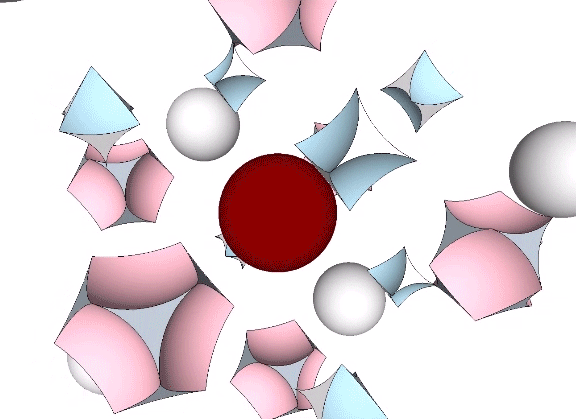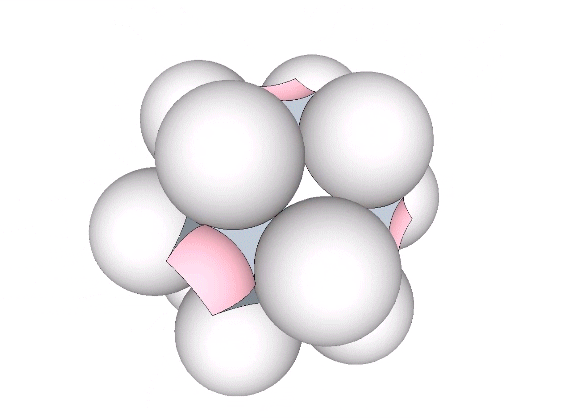
Six spheres close-packed as octahedra surround a nuclear space (“Space”) in the shape of a concave VE, whose volume is slightly less than 1/3 that of the sphere, and slightly more than 1/3 that of the octahedron. The following volumes are all measured in unit tetrahedra. See Areas and Volumes in Triangles and Tetrahedra.

The tetrahedral volume of the concave VE space at the center of six close-packed unit-diameter spheres is the volume of the unit octahedron (4) minus the the volumes of six 1/10 spheres.

Volume of concave VE “space” = 4 – 3π√2/5 ≈ 1.334270237
≈ 33.356755928% the volume of the unit octahedron
≈ 33.298224115% the volume of the unit-diameter sphere

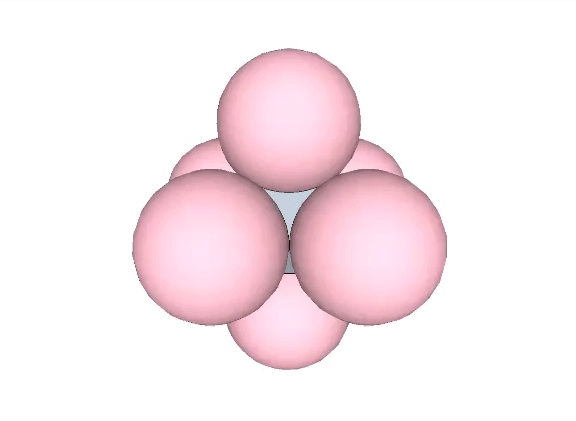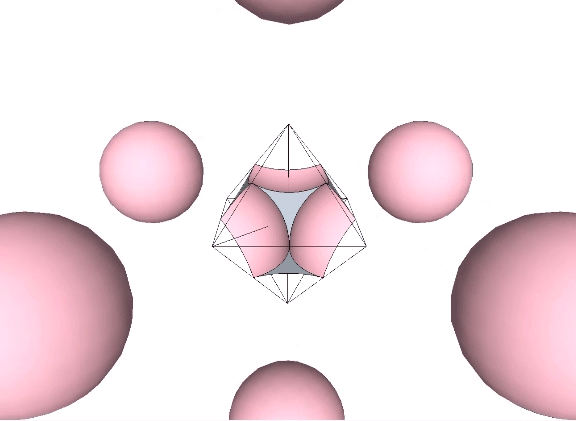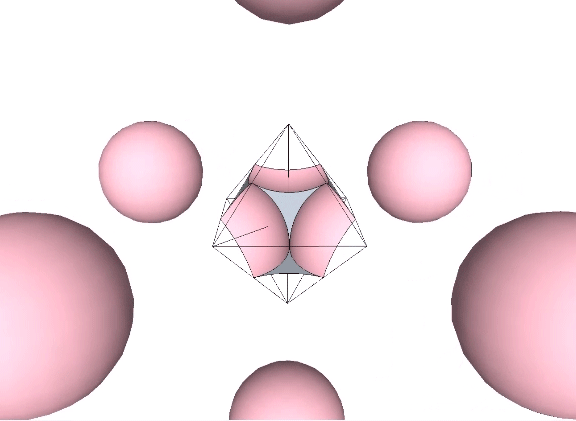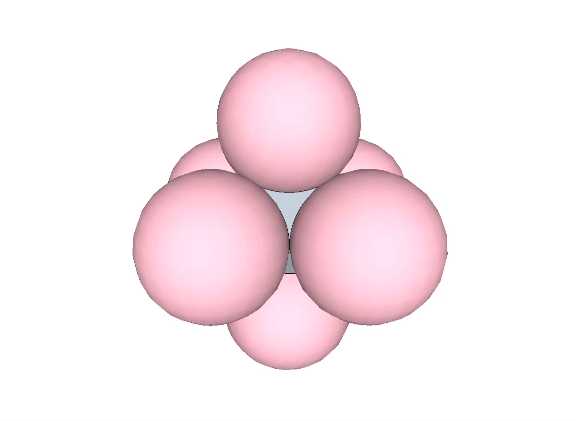
Six close-packed unit spheres constituting the octahedron disperse radially to reveal a concave vector equilibrium (VE) at their common center.
Concave VEs define the “spaces” at the centers of octahedra in the isotropic vector matrix.

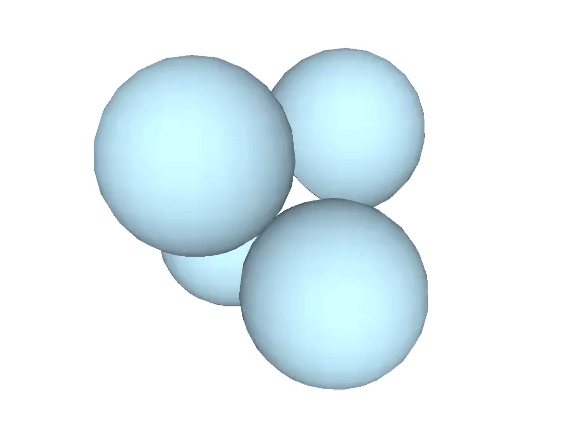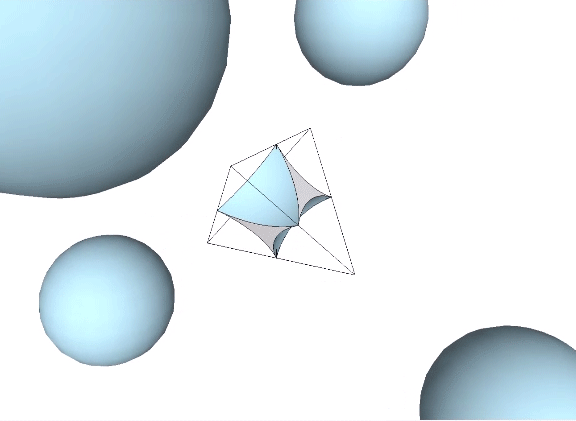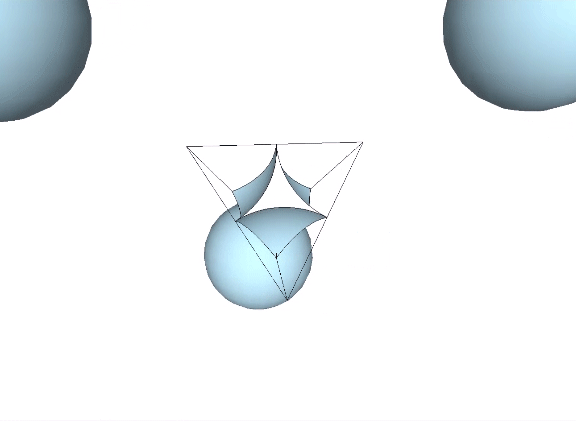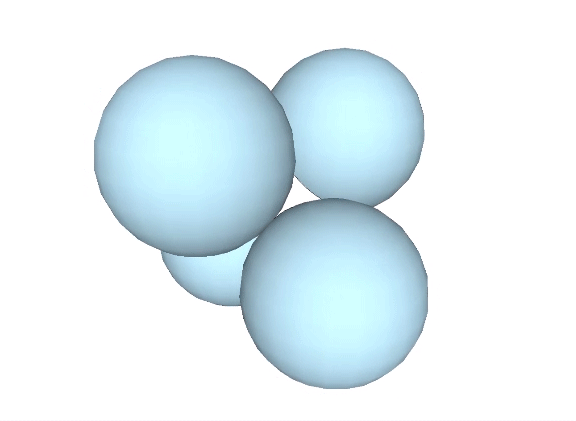
Four spheres close-packed as tetrahedra surround an interstitial space (“Interstice”) in the shape of a concave octahedron, whose volume is a little more than 11% that of the tetrahedron, and a little more than 2.5% that of the sphere.

The tetrahedral volume of the concave octahedron interstice at the center of four close-packed unit-diameter spheres is the volume of the unit tetrahedron (1) minus the the volumes of four 1/20 spheres.

Volume of concave octahedron “interstice” = 1 – π√2/5 ≈ 0.111423412
≈ 11.1423412% the volume of the tetrahedron
≈ 2.5079079% the volume of the sphere

Four close-packed unit spheres constituting the regular tetrahedron disperse radially to reveal a concave octahedron at their common center.
Concave octahedron define the “interstices” between spheres arranged as tetrahedra in the isotropic vector matrix.

The space-to-sphere ratio of the VE is about 44.5/55.5

(6 × volume of concave VE) + (8 × volume of concave octahedron) ≈ 8.00562+ 0.89139 ≈ 8.89701
≈ 44.485043608% the volume of the VE (20)
≈ 25.031631616% the the volume of the VE’s circumsphere (volume about 35.543)

Twelve close-packed unit spheres constituting the vector equilibrium (VE) disperse radially to reveal six concave VEs and eight concave tetrahedra surrounding their common nucleus.
The space between radially close-packed spheres in the isotropic vector matrix is defined by concave VEs and concave octahedra.

The space-to-sphere ratio of the cube is about 31.5%

(5 × volume of concave VE) + (8 × volume of concave octahedron) ≈ 6.67135 + 0.89139 ≈ 7.56274
≈ 31.51142% the volume of the cube (volume 24)

Fourteen close-packed unit spheres constituting the cube disperse radially to reveal twelve concave VEs and eight concave octahedra surrounding a concave VE at their common center.
The space between the close-packed unit spheres constituting the cube is defined by twelve concave VEs and six concave octahedra surrounding a nuclear concave VE space.

In the jitterbug transformation, the spheres and spaces exchange places. The concave VEs become convex VEs (and vice versa) in a transformation that can be described as turning themselves inside-out.

Twelve close-packed unit spheres and six concave VEs surrounding a unit-sphere nucleus exchanging identities in the jitterbug transformation. Spaces become spheres, and spheres become spaces by turning themselves inside-out.
In the jitterbug transformation, spheres and spaces exchange places by turning themselves inside-out.

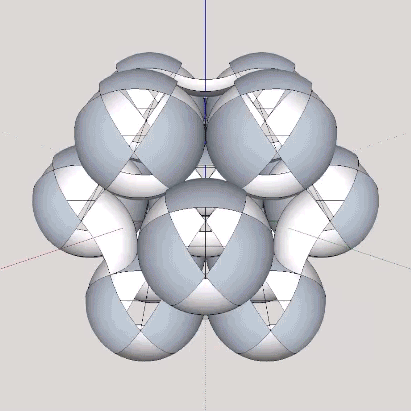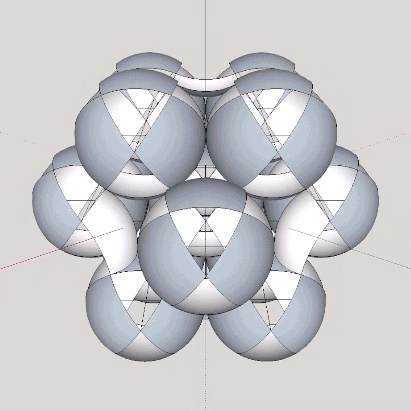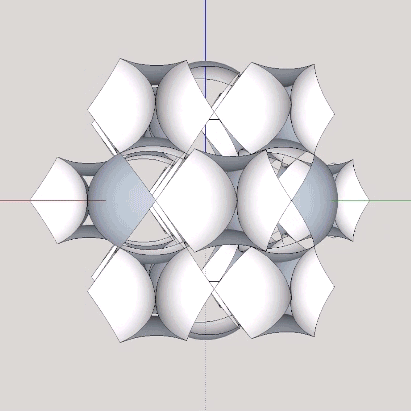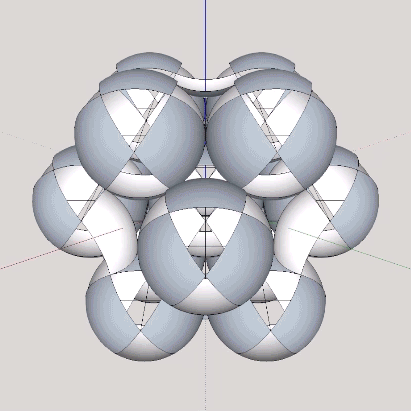
When modeled in quanta modules, the exchange takes place between the two distinct constructions of rhombic dodecahedra, the one found at the center of the VE (the sphere, or convex VE), and the other at the center of the octahedron or cube (the space, or concave VE).

The two alternate quanta module constructions of the rhombic dodecahedron, one representing spheres and other spaces, exchanging identities during the jitterbug transformation by turning themselves inside out.
The sphere-to-space, space-to-sphere inside-outing of the jitterbug transformation modeled with the two quanta-module constructions of the rhombic dodecahedron.

The jitterbug transformation can also be described by the polarity reversal of the tetrahedra. This is manifested in the vector model by the two tetrahedra, one positive, and one negative, that the rotating triangle in the jitterbug alternately describes.

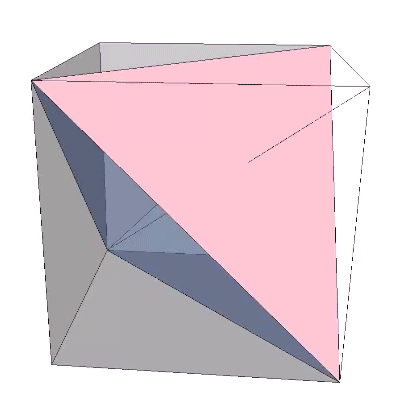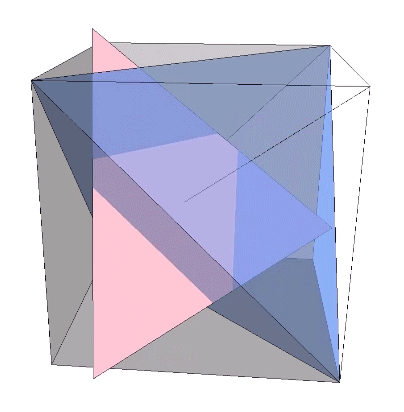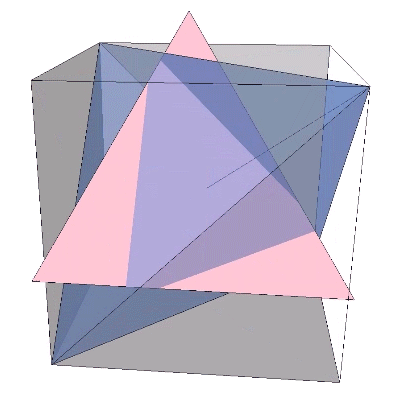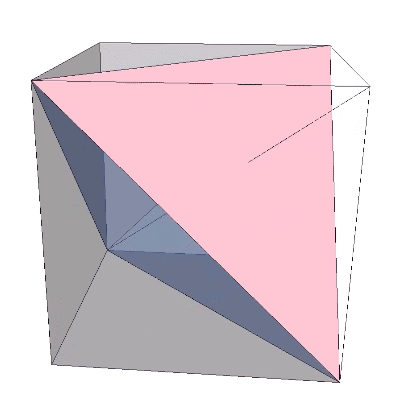
A triangle rotating inside a cube around the cubic diagonal. When its vertices are coincident with the cube's, the triangle constitutes the face of either a positive or a negative tetrahedron.
An isolated triangle from the vector model of the jitterbug transformation alternately defining a positive and a negative tetrahedron.

The polarity reversal of the tetrahedron may be modeled as a 90° rotation. Each tetrahedron is rotated ninety degrees in the transition between the VE and octahedron phases, turning their respective concave octahedron into orientations that describe either a sphere or a concave VE space at their common center.

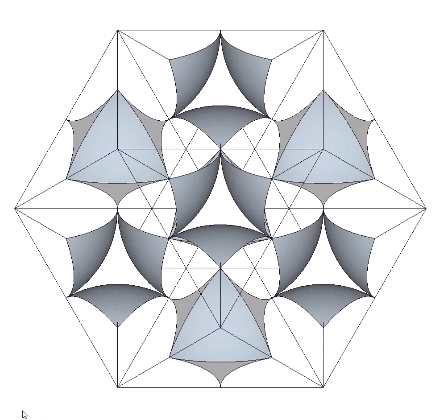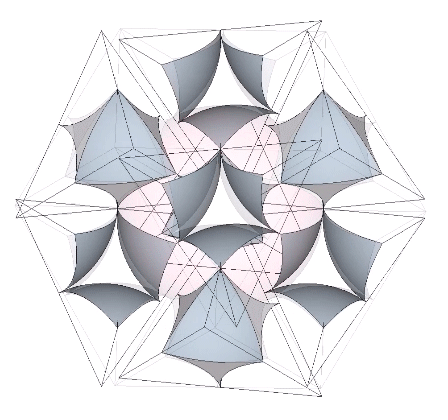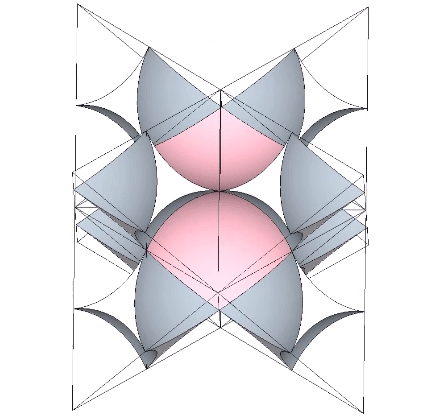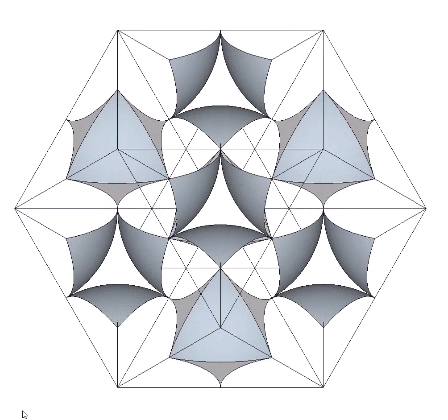
The jitterbug transformation modeled by eight concave octahedra rotating 90° to alternately define a sphere or a space at their common center.
The polarity reversal of the tetrahedra modeled by their 90° rotations in the interstitial model of the jitterbug.

Again, this correlates beautifully with the quanta-module model. Eight quanta-module cubes (each containing a tetrahedron) are rotated 90° to alternately reveal one of the two quanta-module constructions of the rhombic dodecahedron at their common center—one representing the sphere, and one representing the space.

The jitterbug transformation modeled by eight quanta-module cubes. Each cube is rotated 90° and then separated from the others to reveal one of the two quanta-module constructions of the rhombic dodecahedron at their common center.
The polarity reversal of tetrahedra in the jitterbug transformation modeled by the 90° rotation of cubes in the quanta-module model of the jitterbug.

Because the concave octahedron interstices remain constant when the spheres and concave VE spaces exchange places in the jitterbug transformation, their volumes cancel out, and the sphere-to-space ratio of the isotropic vector matrix as a whole is identical with the ratio of volumes of the sphere and concave VE space. That is, the ratio of space to sphere is approximately 2:3.

Leave a comment