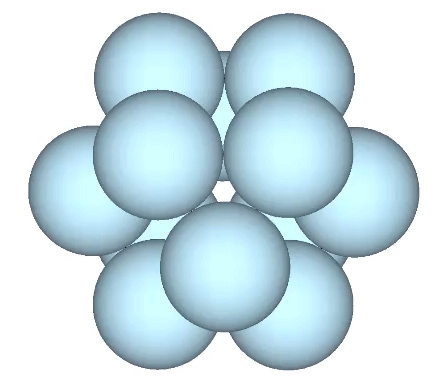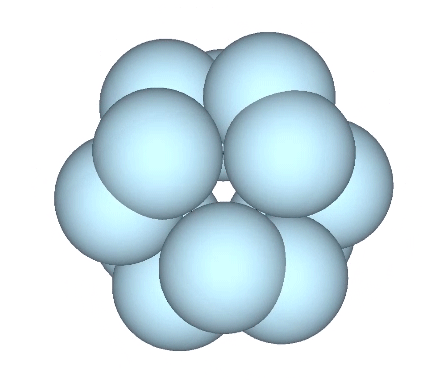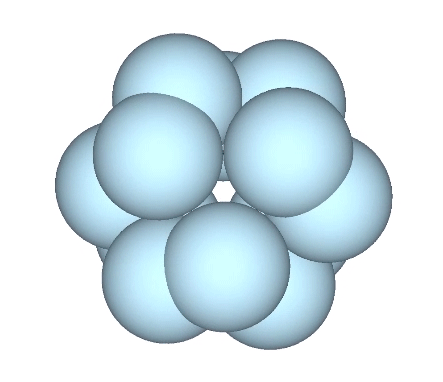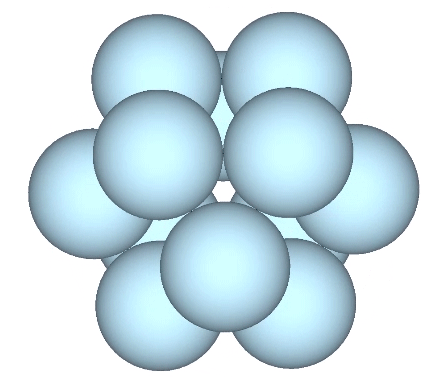
The jitterbug transformation is conventionally modeled as hinged vectors and rotating triangles. But as the vertices are meant to model sphere centers, I’ve here replaced the vertices of the vector equilibrium (VE) with spheres.
The doubling up of edges at the octahedron phase in the vector model of the jitterbug is represented in the sphere model of the jitterbug by merging and diverging unit-radius spheres. Different views and rotations of the model reveal some interesting characteristics of the transformation. If the view is synchronized with the rotation of the top and bottom triangles, the transformation resembles a pump with spheres orbiting around its equator.
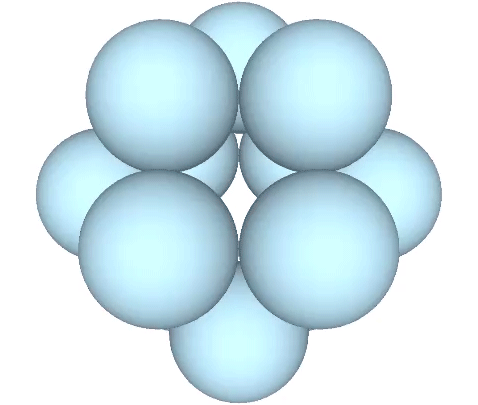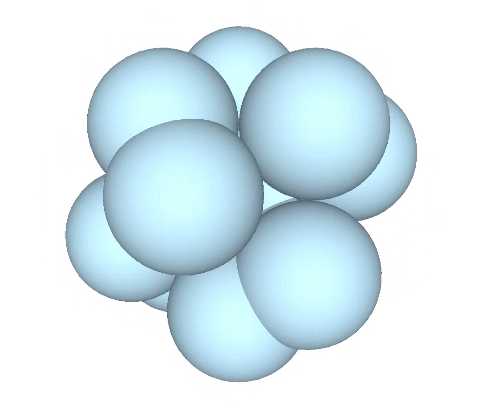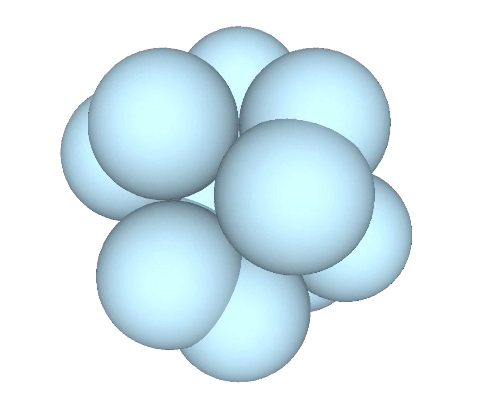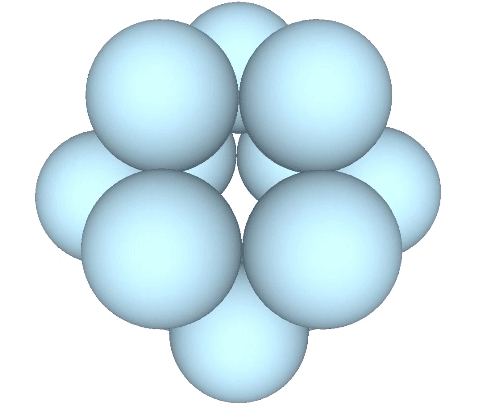
With the view perpendicular to one of the square faces of the VE, and without rotation, the spheres merge and diverge at right angles.
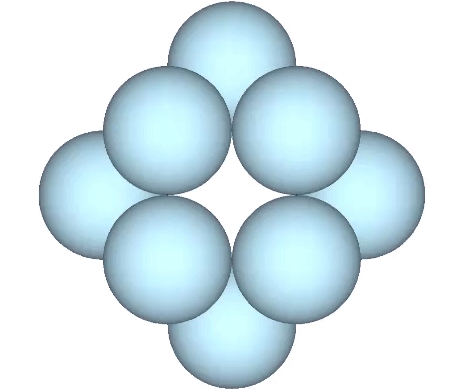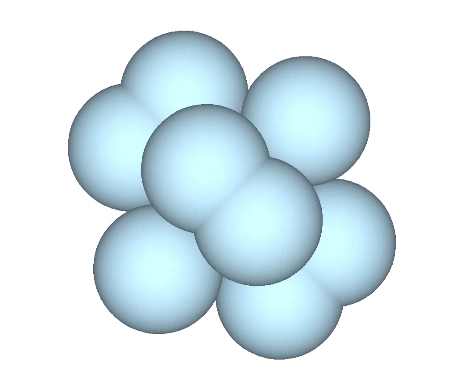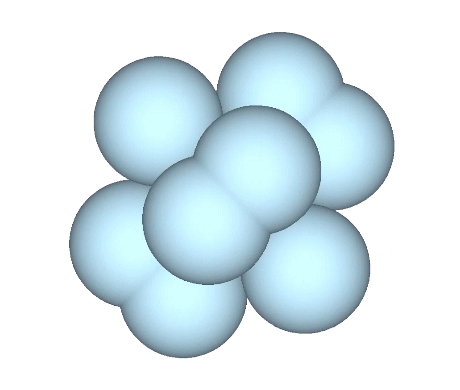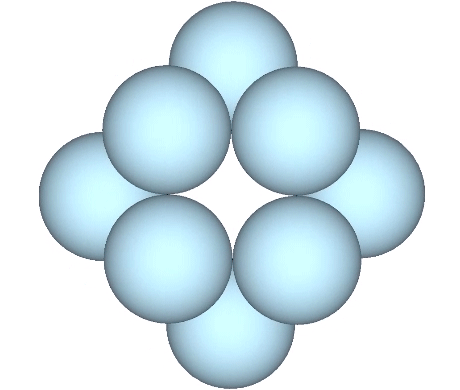
With the view perpendicular to a fixed triangular face, the remaining spheres rotate around the equatorial axis.
The Geometry of Thinking 